SQMS Center

Science Highlights

AI meets quantum: optimal gate compilation using reinforcement learning

The Science: Optimal short gate sequences for quantum state preparation and gate compilation of a noisy qubit using concepts from reinforcement learning and mapped it onto a Markov Decision Process.

The Impact: Compiling arbitrary gates into a fixed discrete gate set and preparing arbitrary initial states in the presence of noise are essential tasks in quantum programming. Tools from reinforcement learning generated solutions that compare favorably to established methods.

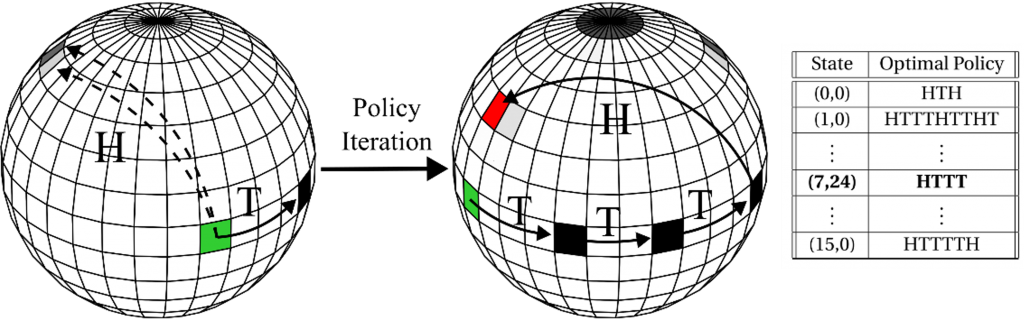
Algorithmic workflow for finding optimal gate sequences for preparing an arbitrary quantum state using concepts from reinforcement learning. By discretizing state space and using a universal gate set such as {H, T, I}, the state preparation task maps onto a Markov Decision Process. Policy iteration yields the optimal policy that generates short gate sequences. 

Summary: Reinforcement learning has been applied to a variety of tasks in quantum programming. The underlying assumption is that those tasks can be modeled as Markov Decision Processes (MDPs). The feasibility of this assumption is tested for two fundamental tasks in quantum programming: state preparation and gate compilation. By forming discrete MDPs and solving for the optimal policy, focusing exclusively on the single-qubit case with and without noise, one finds the shortest possible sequence of gates to either prepare a state, or compile a gate, up to a target accuracy. For example, the sequences of H and T gates with length as small as 11 produce ~ 99% fidelity for states of the form (HT) n||0> with values as large as n = 1010. It is shown that the optimal policy adapts to the effects of noisy gates to achieve a higher state fidelity. The main outcome of this work is that one can impose a discrete, stochastic and Markovian nature to a continuous, deterministic and non-Markovian quantum evolution, which provides theoretical insight and support into why reinforcement learning is expected to be successful in finding optimally short gate sequences in quantum programming.

Contact: Peter Orth – porth@iastate.edu 

Focus Area: Algorithms  

Institutions: Ames National Laboratory, NASA Ames, Rigetti Computing

Alam, M.S., Berthusen, N.F. & Orth, P.P. Quantum logic gate synthesis as a Markov decision process. npj Quantum Inf 9, 108 (2023). https://doi.org/10.1038/s41534-023-00766-w

This work was supported by the U.S. Department of Energy, Office of Science, National Quantum Information Science Research Centers, and Superconducting Quantum Materials and Systems Center (SQMS).