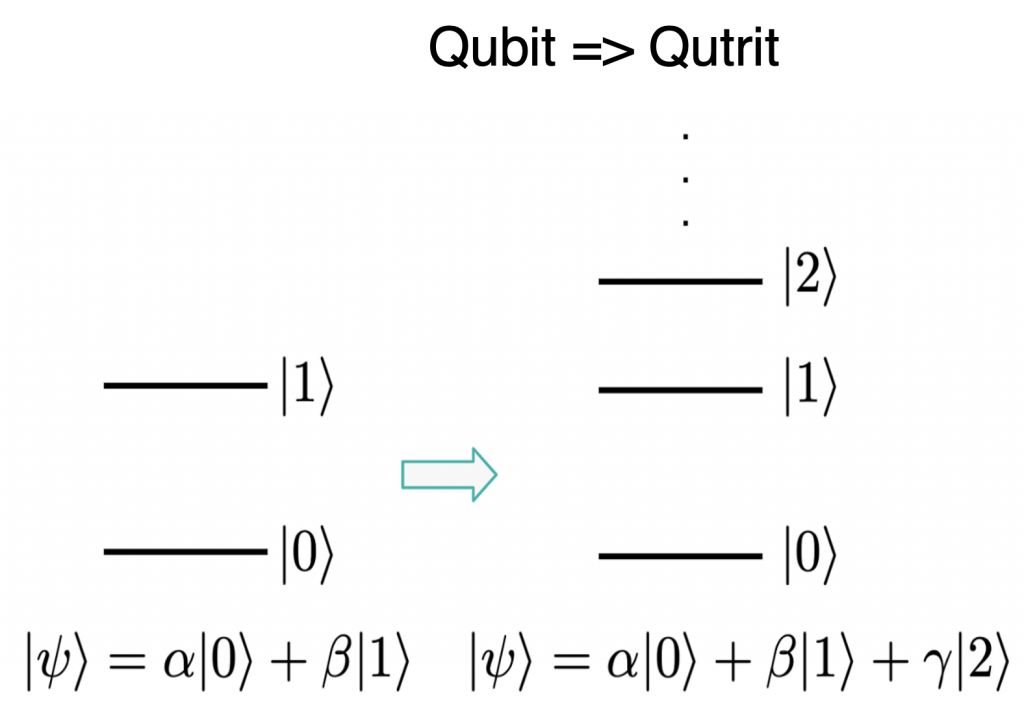Exploring quantum building blocks
Our goals: Pursue device integration and quantum control development for 2D and 3D superconducting architectures to develop quantum computer prototypes with transformational performance in coherence and control.
- Build and deploy quantum computer prototypes based on 3D and 2D architectures
- Build and deploy a 2-meter-diameter dilution fridge to host both the 3D and 2D quantum processors
In this focus area, we use the advances in coherence demonstrated by the materials focus area for both 2D and 3D devices and work to translate those into quantum processor architectures with ultimately higher performance than the state of the art.
Advances in 2D transmon qubits feed into ongoing activities with our industry partner Rigetti Computing, with whom we are co-designing a new processor hand-in-hand that takes advantage of these new fabrication processes.
At the same time, these advances are critical to ensure the 2D qubit ancillas we use for our 3D SRF-based processors are the best possible, enabling us to take full advantage of the 3D SRF high coherence cavities.

Single-cell cavity qubits
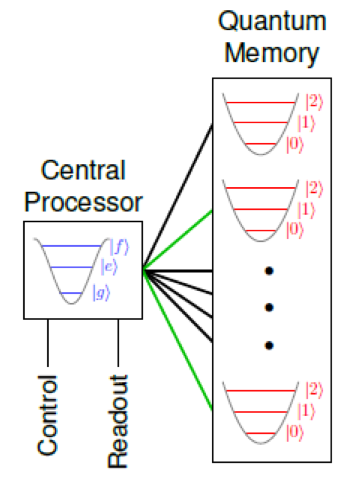
Cavity QED using superconducting cavities is an extension of circuit QED. One challenge in circuit QED is the realization of architectures with high qubit connectivity for the rapidly rising numbers of qubits. Classical computer architectures typically address this challenge using a central processor that randomly accesses a large memory. The two elements often comprise distinct physical systems. A quantum analog realizes a random-access quantum information processor using cQED as processor and quantum memories based on cavity modes.
Quantum behavior in cavities is most obvious in cavity modes excited with specific numbers of energy quanta. But cavity-mode based quantum memory qubits are incapable of logic operations on their own. A single logic-capable processor qubit, such as the transmon, supports many cavity mode-based memory qubits.
This architecture allows control of many highly coherent qubits with minimal electronic overhead to expand the capability to build larger systems. The cavity exhibits a frequency shift dependent on the qubit state.

When it comes to developing a state-of-the-art quantum computer, you must start at the materials level.
This interaction between the qubit and the cavity allows for the exchange of coherent quantum information, as well as enabling entanglement between the two. It is also possible to create large entangled states of this memory using cavity QED with superconducting circuits.
In principle, it is possible to encode with a single transmon up to 14 qubits inside each of the cavity-transmon modules, substantially decreasing the required number of microwave channels for system control and manipulation for a large number of qubits.
Here, the very long (seconds) coherence time in SRF cavity modes, will ultimately allow the creation, control, and manipulation of up to 214 (16,000) microwave photon energy levels, limited by residual nonlinearities and photon loss, instead of using quantum states in the transmon to use quantum states in the resonator, which have higher Q’s and higher coherence times.
With enormous coherence times available with SRF cavities, the absence |0> or presence |1> of microwave photons in specific cavity quantum states has the potential to provide “error-free” cavity-based logical qubits.
It is on these exciting prospects of revolutionizing quantum computing platforms with SRF technology, that we built the vision for the SQMS Center.
Multi-cell cavity qubits
Multimode cavity QED using superconducting circuits and multi-cell cavities can be used as quantum memories to store larger numbers of qubits. This approach has been pioneered and successfully demonstrated by several leading groups, most notably Yale University, to create high-quality factor resonators with 10s of modes with their quantum state controlled by a single Josephson junction circuit. The multiplexed approach can realize a powerful medium-sized quantum processor in the near term.
Yale researchers demonstrated a quantum processor based on controlling 11 coupled 3D cavities with a single transmon. A universal set of quantum gates on 38 arbitrary pairs of modes has been performed and multimode entangled states have been prepared, all using only two control lines. Long-lived quantum memories comprised of bulk, SRF cavities are a particularly enticing architecture toward demonstrating quantum advantage in the near term.
Based on this success, a processor can be implemented, for example with a 9-cell cavity as memory demonstrating universal operations, with a Josephson junction transmon circuit serving as the central processor. The quantum memory is the multimode cavity, using the modes of the 9-cell coupled niobium superconducting resonator. Replacing a system of many two-level qubits by a 9-cell cavity will drastically reduce the hardware cost and complexity requiring fewer components.
However, introducing higher dimensional system with nine modes raises the issue of how to realize complete control over the system, with more complex gates and longer gate times.
As a possible example for the future, the very long coherence in SRF cavities offer transformational advances, ultimately allowing creation, control, and manipulation up to 214 (about 16,000) microwave photon energy levels in each cavity mode (limited by residual nonlinearities and photon loss), which in turn corresponds to 14 qubits for a cavity mode.
This translates to 126 qubits (9×14) for a single mode in the 9-cell SRF cavity. By using two high Q cavities, the corresponding number of cavity qubits could be 2×126=252.
The convolution of a high number of qubits together with dramatically higher quality coherence will result in computers for the quantum advantage era.
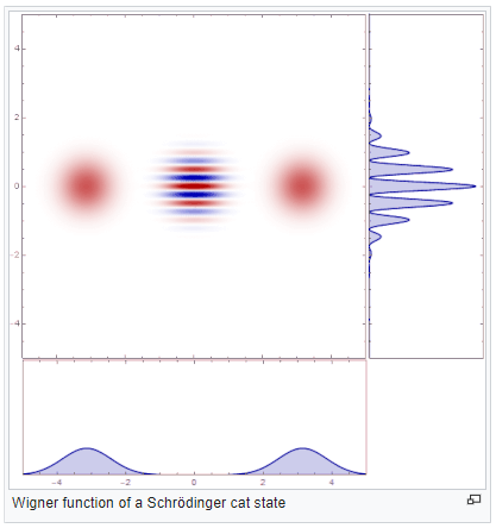
Cat states and error correction
Any quantum superposition of two macroscopically distinct states is called a cat state. For example, consider the interaction between an optical cavity containing a single trapped atom that is in a superposition of two states (“spin up” and “spin down”). When the light pulse in the optical cavity interacts strongly with the atom, the light pulse is brought into a superposition state as well. The light pulse becomes entangled with the atom just as the hypothetical “cat” is entangled with the radioactive atom in Schroedinger’s paradox setup. Consider two quantum cat-states connected via entanglement, for example, via a two-cavity quantum system. Here, the role of each “cat” is played by the light waves, and “life” and “death” roughly correlate to the directions of the electromagnetic field.
Cat states can be used as states of an encoded qubit. The “0” is the electromagnetic wave field at a certain phase (the “living cat”), and the “1” is the field at the opposite phase (the “dead cat”). The atom and light field can both change each other’s state during gate operations.
Yale scientists demonstrated a two-mode cat state of electromagnetic fields in two microwave cavities bridged by a superconducting artificial atom (Josephson junction), which can also be viewed as an entangled pair of single-cavity cat states.
Cat states provide an attractive approach for redundantly encoding quantum information for error correction with minimal overhead. Qubits based on cat states, or bosonic qubits, can be controlled by fewer error-prone ancilla qubits (extra measurement qubits) due to the inherent symmetry of the multi-photon state.
Error-corrected ancilla-enabled gates are an important step towards fully fault-tolerant processing of bosonic qubits.
One key technique is the ability to measure whether the cat state has an even or odd number of photons, i.e to measure the odd or even parity of the cat state, without measuring the photon number. For example, photon loss is an error that flips parity, which results in an observable shift of the qubit frequency. So, it is possible to detect this error without perturbing the encoded information.
Yale scientists have successfully harnessed and manipulated 100 microwave photons into Schrödinger cat states, which could serve as entangled qubits.
With a 9-cell SRF cavity and advanced transmon qubits, it should be possible in principle to generate unprecedently large microwave cat states to provide a large number of entangled qubits for error-free quantum computing.
Qudits
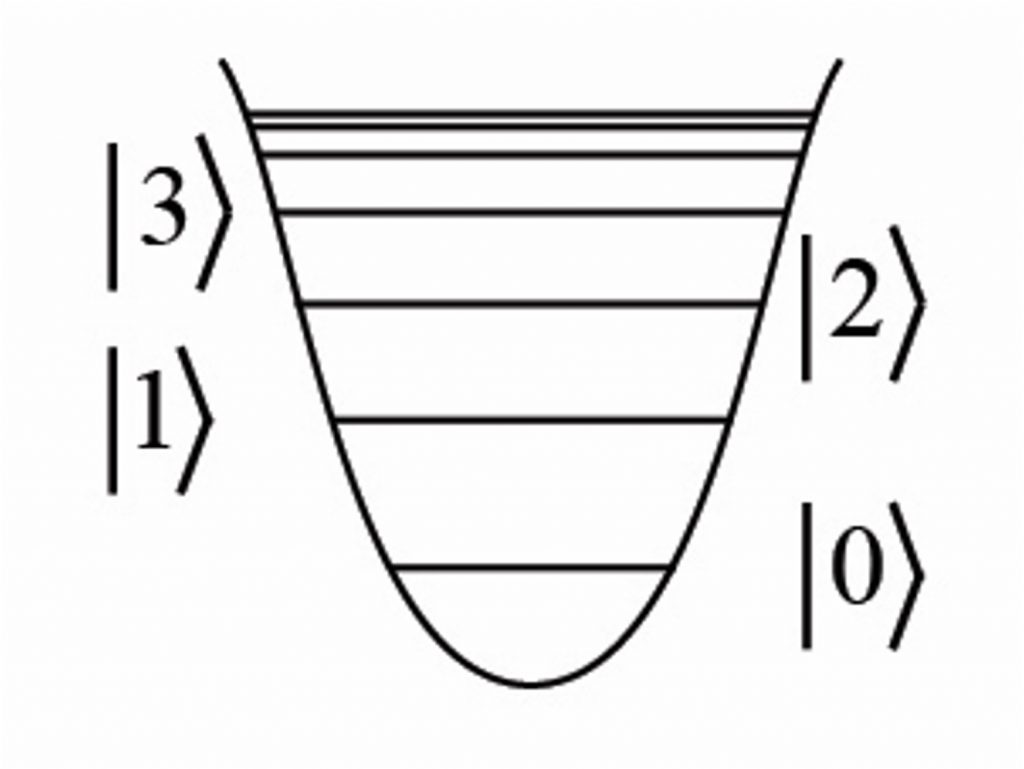
Qudits are quantum entities in which the number of possible states is D, which can be 3, 4, 5…as long as D is greater than two (as for qubits). A qudit is a generalization of the qubit to D-dimensional space. When D = 3 the quantum entities are called qutrits, with three states; with D = 4 there are four states and the quantum objects are ququarts, and so on.
For every added state, the processing ability of a single qudit increases so that you need fewer qudits than qubits to encode and process the same amount of information.
As a specific example, the qutrit is based on a 3-state quantum system, such as the 3 energy levels of an atom, or 3 photon wavelengths in the three modes of a three-cell superconducting cavity. The basis for the qutrit is 0, 1, 2, instead of 0 and 1 for a qubit. The qutrit offers a more efficient way to represent data than the binary qubits. For example, with qutrits, the number 65 can be written as 2×33 + 1×32 + 0x31 + 2×30, as 2102, instead of the longer 1000001 = 1×20 + 0x21 + 0x22+ 0x23 +0x24 + 0x25 + 1×26 in the binary system.
Qudits offer computing power exponentially more than qubits. Since a qubit exists as a superposition of two states a pair of qubits can perform four operations. Adding a third qubit increases to eight operations. Multilevel qudits provide the potential to simplify computational tasks as well as the circuitry required to realize the quantum computer.
Instead of working with a large number of qubits to reach high processing capabilities, it may turn out more feasible to maintain a smaller number of qudits, with each holding a greater range of values to optimize computations.
Qudits also offer a dramatic reduction in the number of the required microwave channels to only one input per hundred effective qubits. However, it is more challenging to manipulate qudits than qubits.